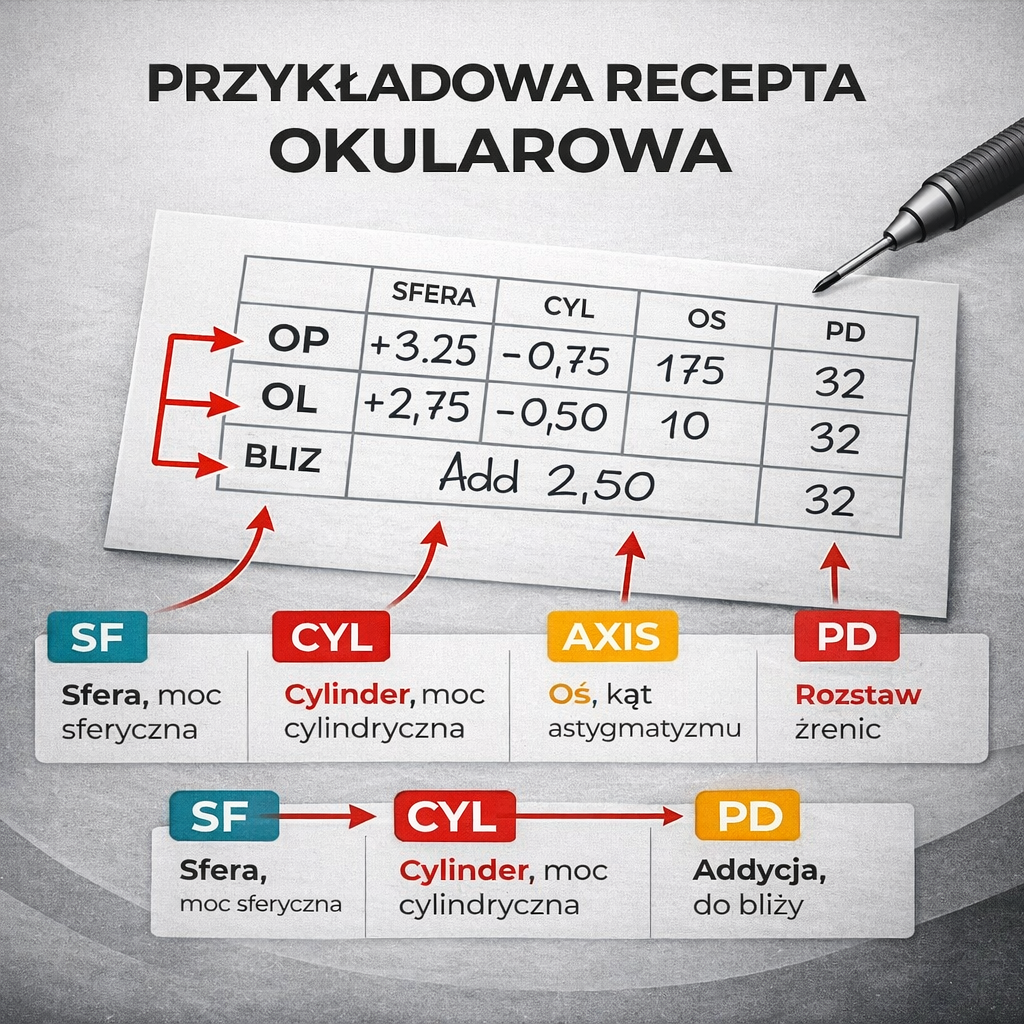
Jak odczytać receptę okularową?
Na receptach okularowych stosuje się uniwersalny zapis mocy korekcji wady wzroku w kilku kolumnach.
Kolumna nr 1 – Sfera (SPH) służy do określenia mocy szkieł do dali lub bliży, czyli zdolności oka do skupiania promieni na siatkówce. Jest określana w dioptriach sferycznych co 0,25. Ujemna sfera (-) oznacza krótkowzroczność oraz potrzebę zamontowania soczewki okularowej o zdolnościach rozpraszających. Dodatnie wartości sfery (+) wskazują na dalekowzroczność. Możemy się również spotkać z zapisem “0”, bądź PLAN oznaczającym brak potrzeby sferycznej korekcji okularowej w danym oku.
Kolumna nr 2 – Cylinder (CYL) to parametr określający stopień korekcji astygmatyzmu, wady związanej z nieprawidłową krzywizną rogówki bądź soczewki. Zapis ma wartość dodatnią lub ujemną, obliczaną z dokładnością do 0,25 dioptrii. Zmiana znaków cylindra nie oznacza odmiennych mocy szkieł.
Kolumna nr 3 – Oś (AXIS) musi być podana w celu właściwego ustawienia soczewki cylindrycznej. Jej wartości zawierają się w przedziale od 0° do 180° i występuje jedynie wraz z wartościami cylindrycznymi
ADD – addycja czyli dodatek do bliży. Przykładowo przy korekcji do dali +1.5 dptr i addycji (ADD) +2 oznacza to że potrzebujesz korekcji do bliży o mocy +3.5 dptr
Jak odczytać receptę okularową wystawioną poza Polską
OP: -1,00 / -0,25 / 70
OL: -1,50 / -0,50 / 110
Jednocześnie poniższy zapis jest równoważny z tym z recepty:
OP: -1,25 / +0,25 / 160
OL: -2,00 / +0,5 / 20
PD – Pupil distance = rozstaw źrenic
Zmiana znaków cylindra oraz osi nie oznacza innych mocy szkieł. Zapis każdego rodzaju szkieł cylindrycznych możliwy jest w dodatnim bądź ujemnym cylindrze.
Jak przeliczyć szkła cylindryczne plus na minus i minus na plus
1. Najprostszy sposób to zapis TYLKO mocy sferycznych, np.: sf +2,00 dptr. lub każda inna moc w zakresie od: 0,00 (inaczej PLAN) do +/- 30,00! (nawet więcej…)
2. Sprawa się komplikuje w przypadku mocy cylindrycznych. Tutaj pojawia się magiczne przeliczanie mocy szkieł. Weźmy naszą sferę z pkt.1 i dodajmy do niej cylinder, np. +1,50 dptr. Otrzymamy zapis:
sf: +2,00/cyl: +1,50 i ZAWSZE MUSI BYĆ OŚ – np. 45o
ten sam zapis można przekształcić do postaci:
sf: + 3,50/cyl: -1,50 oś 135o
Co się stało? Dodaliśmy sferę do cylindra – otrzymaliśmy + 3,50 dptr; zmieniliśmy znak cylindra na przeciwny (z „+” na „-„) NIE ZMIENIAJĄC jego wartości bezwględnej i zmieniliśmy oś cylindra o 90o. Oś CYLINDRA zawsze musi mieć wartość pomiędzy 0o a 180o